名刺にも使われる黄金比…と題していますが、一般的な名刺は55×91mmで、細かいことをいうと若干、黄金比より短辺が短い、もしくは長辺が長いのです。しかし細かいことは気にしないで本文に入ります。
黄金比は、レオナルド・ダ・ヴィンチなど多くの芸術家や建築家が使っていたとされる、最も美しいと言われている比率です。
この比率は、約1:1.618で、数学的には、a,bで分割した場合にa:b=b:(a+b)が成り立つ比率ということになります。
黄金比は、画面の分割や縦横比に用いられるほか、画面内の様々な要素にも使われます。また、彫刻や建築などにも用いられています。
例えば、ダ・ヴィンチのモナ・リザの顔は横1:縦1.618の黄金比の長方形にピッタリはまり、葛飾北斎の冨嶽三十六景「神奈川沖浪裏」は黄金比のほか三分割法も用いられています。ピラミッドの高さと底辺は1:1.618、パルテノン神殿の縦横比なども1:1.618だといいます。
古くから発見され用いられてきた黄金比は、ビジュアル的に存在感や安定感をもたらすだけでなく、それ以上の不思議なパワーを持つ比率なのでしょう。
そのパワーにあやかるべく、何を隠そう、私の愛車のナンバーも黄金比です…なんのこっちゃ…(..;
では、その黄金比がどのような性質を持って、どのように不思議なのか…。
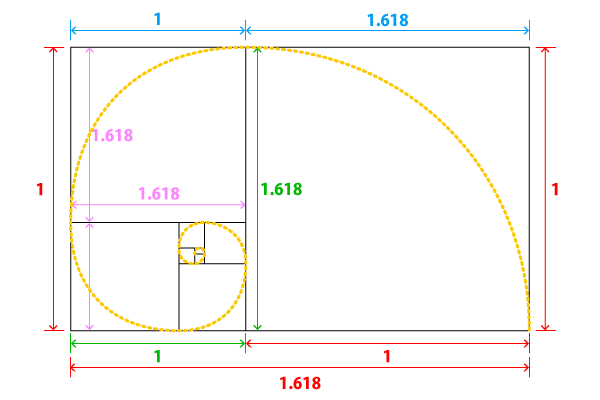
下記の画像は黄金比の長方形(赤字の比率)です。
長辺を黄金比1:1.618で分割しますと(青字の比率)、縦横1:1の正方形(右側/赤字の比率)と黄金比の長方形(左側/緑字の比率)が出来ます。
その分割された黄金比の長方形をまた黄金比で分割しますと…無限に黄金比の長方形が出来るわけです。
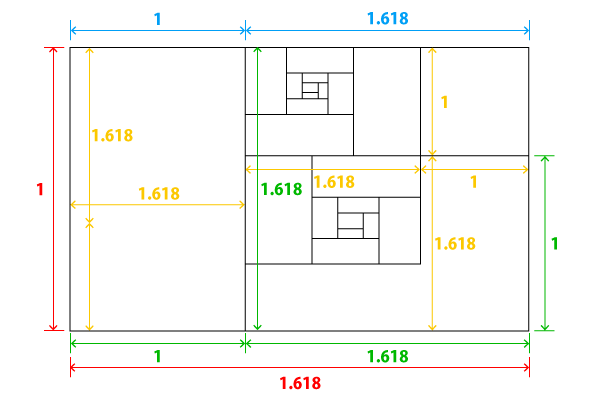
黄金比は、右側の正方形にも無限にあります(下図)。
正方形を黄金比で分割しますと(黄字の比率/この場合は上下)、この場合は下に黄金比の長方形ができ、あとは上記と同じく無限に繰り返します。
上の長方形を黄金比で分割しますと(黄字の比率/この場合は左右)、黄金比の長方形(左側)と正方形(右側)ができ、あとは無限ループです。
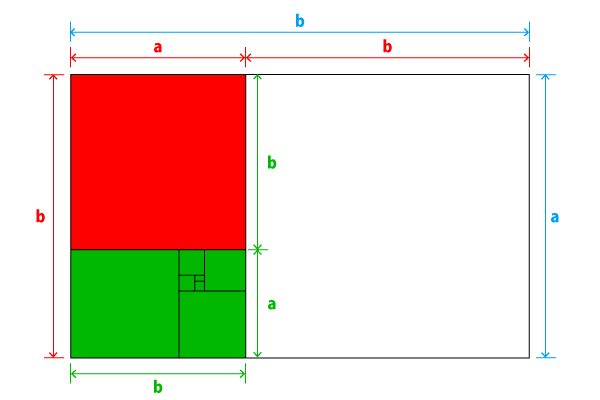
下の図は比率をa,bで表してみました。
青字の比率a:b=赤字の比率b:(a+b)となります。赤字の比率a:b=緑字の比率b:(a+b)となります。
こういう現象は、他の比率では起こらないので、なんだか不思議な感じがしますねぇ~。
ピッタリ黄金比とはいかなくても、ほぼ黄金比は生活の中に溢れています。
特段意識しなくても、ビジュアルが美しいということは、知らず知らずのうちに誰もが黄金比を使っているかもしれません。



コメント